SLOs
1- Students are able to understand what is Real Numbers.
2-Types of Real Numbers.
3- what is Rational Numbers.
4- What is Irrational numbers.
5- Difference between Rational Numbers and Irrational numbers.
Real Numbers
Simply we define the Real numbers as :
The combination of Rational and Irrational numbers OR The Union of Rational and Irrational numbers are called Real numbers, and Real numbers are denoted by capital R ,
Rational numbers are denoted by Q
Irrational numbers are denoted by Q'
So R = Q+Q'
OR R=Q U Q'
Examples:
3/7 , √16 , -3/2, 0, √(16/81) , 8/11,25,7,√27, √25, π (Pai), 245674, 0.43245667
Real Numbers
Real numbers are the set of numbers that include both rational numbers (numbers that can be expressed as a ratio of two integers) and irrational numbers (numbers that cannot be expressed as a ratio of two integers, such as √2 or π). The set of real numbers is represented by the symbol R. Real numbers can be represented on a number line, and can be positive, negative, or zero. They are used in many areas of mathematics, including calculus and linear algebra.
OR
Real numbers are the set of numbers that include both rational numbers (numbers that can be expressed as a ratio of two integers) and irrational numbers (numbers that cannot be expressed as a ratio of two integers, such as √2 or π). The set of real numbers is represented by the symbol R. Real numbers can be represented on a number line, and can be positive, negative, or zero. They are used in many areas of mathematics, including calculus and linear algebra.
More about real numbers
Real numbers are a fundamental concept in mathematics, and have a wide range of applications in science, engineering, and other fields. They are used to represent quantities that can take on any value within a certain range, such as distance, temperature, or time.
Real numbers can be classified into several different types, including:
Natural numbers:
The set of positive integers, often represented by the symbol N.
Whole numbers:
The set of natural numbers, including zero, often represented by the symbol W.
Integers:
The set of whole numbers and their negatives, often represented by the symbol Z.
Rational numbers:
Numbers that can be expressed as a ratio of two integers, such as 2/3 or -5/7.
Irrational numbers: Numbers that cannot be expressed as a ratio of two integers, such as √2 or π.
Real numbers also have certain properties and behaviors, such as:
Closure property:
The set of real numbers is closed under the operations of addition, subtraction, multiplication, and division (with the exception of division by zero).
Commutative property:
The order of the numbers being added or multiplied does not affect the result.
Associative property:
The way the numbers are grouped in an addition or multiplication does not affect the result.
Identity element:
0 is the identity element for addition, and 1 is the identity element for multiplication.
Real numbers are used in many areas of mathematics, such as algebra, geometry, and calculus. They are also used in physics, engineering, economics, and other fields to model and analyze real-world phenomena.
:حقیقی اعداد
ایسے اعداد جو ناطق اعداد اور غیر ناطق اعداد کا مجموعہ ہوں۔ ایسے اعداد حقیقی اعداد کہلاتے ہیں۔
ناطق اعداد کو ظاہر کرنے کے لیے ہم جو علامت استعمال کرتے ہیں وہ
Q.
اور غیر ناطق اعداد کو ظاہر کرنے کے لیے ہم جو علامت استعمال کرتے ہیں وہ
Q'
Rational Numbers
The numbers that can be written in the form of p/q, where p,q are the integers (Z=.....-3,-2,-1,0,1,2,3,4....) and q is not equal to zero.
ناطق اعداد:
ایسے اعداد جن کو ہم
p/q
کی شکل میں لکھ سکیں یا ایسے اعداد جن کو کسر کی شکل میں لکھ سکیں
.p,q
کا تعلق صحیح اعداد سے ہے۔اور
q
صفر نہیں ہونا چاہیے
Examples of Rational numbers:
3/2 , 4 , 7/9 , 22/7 , 1.735 , 2.7657 , √25 , √4 (under root of the numbers which are perfect square ) etc are the examples of Rational numbers.
Definition of Rational Numbers
Rational numbers are numbers that can be expressed as the ratio of two integers, where the denominator is not equal to zero. These numbers can be represented as fractions, such as 3/4 or -5/2, and can also be represented as decimal numbers that either terminate (such as 0.75) or repeat (such as 0.666...). Examples of rational numbers include -1, 0, 1/2, 3/4, and 22/7 (which is a common approximation of pi). All integers are also considered to be rational numbers.
More about rational numbers
Rational numbers are closed under the operations of addition, subtraction, multiplication, and division, as long as the divisor is not zero. This means that if you add, subtract, multiply, or divide two rational numbers, the result is always another rational number. For example, if you add 1/2 and 3/4, the result is 5/4, which is a rational number.
Rational numbers can also be represented in decimal form, either as a terminating decimal (such as 0.75) or as a repeating decimal (such as 0.666...). A rational number will always have a terminating decimal representation if its denominator is a power of 10, such as 10, 100, or 1000, and it will always have a repeating decimal representation if its denominator is not a power of 10.
It is important to note that not all numbers can be represented as rational numbers. For example, numbers like pi and the square root of 2 are not rational numbers and are known as irrational numbers.
Rational numbers are also important in many branches of mathematics such as number theory, algebra and geometry. They are used in many different areas of science and engineering, as well as in everyday life.
More examples
Here are some more examples of rational numbers:
1/3 (this is a fraction where the numerator is 1 and the denominator is 3)
-2 (this is an integer, which is considered to be a rational number)
0.25 (this is a decimal representation of the fraction 1/4)
-0.6 (this is a decimal representation of the fraction -3/5)
5 (this is an integer, which is considered to be a rational number)
2.5 (this is a decimal representation of the fraction 5/2)
100/7 (this is a fraction where the numerator is 100 and the denominator is 7)
-8/3 (this is a fraction where the numerator is -8 and the denominator is 3)
12.75 (this is a decimal representation of the fraction 51/4)
-3.14 (this is a decimal representation of the fraction -157/50)
As you can see, rational numbers can be expressed as both fractions and decimals. They can be positive or negative, and can be expressed as integers, fractions, or decimals.
Is pie is irrational number
Yes, pi (π) is an irrational number. An irrational number is a number that cannot be expressed as the ratio of two integers. It cannot be represented as a terminating decimal or a repeating decimal. Instead, its decimal representation goes on forever without repeating.
Pi is the ratio of a circle's circumference to its diameter and is an important mathematical constant that appears in many formulas in geometry and trigonometry. Its decimal representation starts as 3.14159265358979323846... and goes on indefinitely without repeating. It's also a non-repeating non-terminating decimal number.
While pi can be approximated by rational numbers like 22/7, but it is not a rational number itself. Since pi is not a ratio of two integers it is considered to be irrational number
Irrational Numbers :
The numbers that cannot be written in the form of p/q, where p,q are the integers (Z=.....-3,-2,-1,0,1,2,3,4....) and q is not equal to zero.
غیر ناطق اعداد:
ایسے اعداد جن کو ہم کسر کی شکل میں نہیں لکھ سکتے غیر ناطق اعداد کہلاتے ہیں۔
Examples of Irrational Numbers :
√3 , √3/4 , 1.123123123..... , √7 , π ,etc are the examples of Irrational Numbers.
( Under root of the numbers which are not perfect square are also Irrational numbers )
Rational Numbers are also define as :
The decimals which are non terminating and non repeating are known as Irrational numbers.
غیر مختتم اور غیر متوالی کسر اعشاریہ کو ہم غیر ناطق اعداد کے نام سے جانتے ہیں۔
Operations on Rational numbers:
Now we perform operations on Rational numbers like addition, subtraction, multiplication and division.
Addition of Rational numbers:
ناطق اعداد کی جمع
Let x/y and a/y are two rational numbers with different nominator and same denominator, then we add these rational numbers as following.
x/y + a/y = ( x +a )/y
Now we solve some examples:
1) 7/5 + 1/5
= (7+1)/5
=8/5 ans.
2) -1/7 + 2/7 + 4/7
= ( -1+2+4 )/ 7
= 5/7 ans
3) 12/5 + 7/5 + (-14)/5
= ( 12+7-14) / 5
= 5/5
= 1 ans
If a/b and x/y are two rational numbers. There numerator شمار کنندہ and denominator مخرج both are different then we following formula to add them.
a/b + x/y = ( ay + xb)/yb
Now we solve some examples.
1) -6/5 + 8/12
= ( -72 + 40 )/60
= - 32/60
= -16/30
= -8/15 ans
2) 4/3 + 5/2 + 3/4
= ( 16+30+9)/12
= 55/12 Ans
Subtraction of Rational numbers:
ناطق اعداد کی تفریق
Let x/y and a/y are two rational numbers with different numerator and same denominator, then we subtract these rational numbers as following.
x/y - a/y = ( x - a )/ y
Now we solve some examples.
1) 3/7 - 1/7
= ( 3 - 1 ) / 7
= 2/7 ans
2) 8/9 - 1/9 - ( -4/9)
= ( 8-1+4 )/ 9
= 11/9 ans
If a/b and x/y are two rational numbers. There numerator and denominator both are different then we following formula to add them.
a/b - x/y = ( ay - xb )/ yb
Now we solve some examples.
1) 5/4 - ( - 7/8)
= 5/4+7/8
= ( 10 + 7 )/8
= 17/8 ans
2) 5/2 - 3/4 - ( -1/8)
= 5/2 - 3/4 + 1/8
= ( 20 - 6 + 1 )/8
= 15/8 ans
Additive Inverse:
جمعی معکوس
Suppose that x/y and - x/y are two rational numbers and if we add these both rational numbers then
x/y + ( -x/y) = ( - x/y ) + x/y = 0
We note that the sum of these two rational numbers is 0 . These two rational numbers (x/y) and ( -x/y ) are called additive Inverse of each other and zero (0) is known as additive Identity. جمعی ذاتی عنصر
Examples:
2 and -2 are additive Inverse of each other
-1/3 and 1/3 are additive Inverse of each other
7/4 and -7/4 are additive Inverse of each other
-5 and 5 are additive Inverse of each other
In above examples we note that if we add both numbers in each example the result is zero (0).
Multiplication of Rational numbers:
ناطق اعداد کی ضرب
In multiplication of rational numbers we multiply the numerator of one rational number by the numerator of other rational number and multiply the denominator of 1st rational number by others denominator.
i.e p/q × t/f = pt / qf
Examples:
4/6 × 5/3 = (4×5) / (6×3) = 20/18 = 10 / 9 ans
1/4 × (-2/3) ×(-5/2) = +10/24 = 5/12 Ans
Multiplicative Inverse : ضربی معکوس
Suppose two non zero rational numbers x/y and y/x and if we find the product as
x/y × y/x = 1
We note that the product of these two rational numbers is 1 so these two rational numbers are known as multiplicative Inverse of each other and 1 is called the multiplicative Identity.ضربی ذاتی عنصر
Examples:
3 and 1/3 are multiplicative Inverse of each other
-6 and - 1/6 are multiplicative Inverse of each other
3/2 and 2/3 are multiplicative Inverse of each other
-7/9 and -9/7 are multiplicative Inverse of each other
In above examples we note that if we multiply both numbers the result is 1 and 1 is called multiplicative Identity.
Note :
For any non zero rational number x/y the rational number y/x is called its reciprocal.
The number zero (0) has no reciprocal.
Division of Rational numbers:
ناطق اعداد کی تقسیم
We know that division is an inverse operation of multiplication so we understand the division process by following examples.
6/3 ÷ 12/3 = 6/3 × 3/12 = ( 6×3)/(3×12) = 1/2 Ans
3/5 ÷ (-6/5) = 3/5 × (-5/6) = -15/30 = -1/2 Ans
Properties of Rational Numbers:
1-Commutative property w.r.t Addition:
قانون مبادلہ بلحاظ جمع
Suppose p/q and r/s are two rational numbers then Commutative property of addition is
p/q + r/s = r/s + p/q
Example:
2- Commutative property w.r.t Multiplication:
قانون مبادلہ بلحاظ ضرب
Suppose p/q and r/s are two rational numbers then Commutative property of multiplication is
p/q × r/s = r/s × p/q
Examples:
Associative property:
1- Associative property w.r.t Addition:
قانون تلازم بلحاظ جمع
Suppose that p/q , r/s and t/u are three rational numbers then the associative property of addition is
(p/q + r/s) + t/u = p/q +(r/s + t/u)
Examples:
2- Associative property w.r.t Multiplication:
قانون تلازم بلحاظ ضرب
Suppose that p/q , r/s and t/u are three rational numbers then the associative property of multiplication is
(p/q × r/s) × t/u = p/q × (r/s × t/u)
Examples:
Distributive Property of Multiplication over addition:
قانون تقسیمی بلحاظ جمع
Suppose that p/q , r/s and t/u are three rational numbers then the distributive property is
p/q × ( r/s +t/u) = ( p/q ×r/s ) + ( p/q × t/u )
Example:
1/5 × (9/10 +1/2) =( 1/5×9/10) + (1/5 × 1/2 )
Distributive Property of Multiplication over subtraction:
قانون تقسیمی بلحاظ تفریق
Suppose that p/q , r/s and t/u are three rational numbers then the distributive property is.
p/q × ( r/s - t/u) = ( p/q × r/s ) - ( p/q × t/u )
Example:
1/4 × ( 1/2 - 1/6 ) = ( 1/4 × 1/2 ) - ( 1/4 × 1/6)
Frequently asked questions (FAQs)
1-What is real number example?
The real numbers (R) are numbers which include both rational (Q) and irrational (Q') numbers.The rational numbers (Q) are such a integers (-2, 0, 1), fractions(1/2, 2.5) and irrational numbers (Q') such as √5, π(22/7), etc. are all real numbers.2-What is meant by real numbers?
In mathematics real number is a quantity that can be expressed as an infinite decimal expansion. The real numbers include the positive (+) and negative(-) integers (Z) and fractions (or rational numbers) and also the irrational numbers.
3-What are all the real numbers?
The numbers 28, -198.5, 0, 32/9 and 5 balls are all real numbers. Strangely enough, numbers such as √3 (the square root of 3) the value of which is 1.7320...) and π (3.1415...) can be plotted on the number line as well, even though they are non-terminating decimal numbers.4-What is set of real numbers?
The set of real numbers (R) includes every number, positive(+), negative(-) and decimal(.) included, that exists on the number line. The set of real numbers is represented by a symbol capital R . The set of integers includes all whole numbers (positive+ and negative-), including 0 . The set of integers is represented by the symbol capital (Z) .5-What are examples of not real numbers?
Which Numbers are not Real Numbers? Complex numbers, like ⎷-1 or √-3 etc are not real numbers. In other words we say, the numbers that are neither rational nor irrational, are called not real numbers.6-How do you know if it's all real numbers?
One identifying characteristic of real numbers(R) is that they can be shown over a number line. Think of a horizontal line. The center point, or the origin, or mid point is zero(0). To the right side are all positive(+) numbers, and to the left side are the negative points.
7-Is irrational number a real number?
The irrational number(Q'), any real number that cannot be expressed as the quotient of two integers as x/y. Each irrational number can be expressed as an infinite decimal expansion with no regularly repeating digit( for example 0.2431508765......) or group of digits. Together with the rational numbers(Q); they form the real numbers.real numbers definition
real numbers list
real numbers definition and examples
rational numbers examples
rational numbers definition
rational numbers meaning
rational numbers properties
rational numbers and irrational numbers
rational numbers list
rational numbers calculator
irrational numbers definition
irrational numbers list
irrational numbers symbol
irrational numbers definition with examples
irrational numbers meaning
additive inverse
additive identity
additive inverse property
additive identity property
additive and subtraction of rational numbers
additive inverse of rational numbers
additive identity of rational numbers
addition of rational numbers
multiplicative inverse
multiplication of rational numbers
multiplicative identity property
multiplication
multiplication and division of rational numbers
Properties of Rational Numbers
Commutative property w.r.t Addition
Commutative property w.r.t Multiplication
Associative property
Have a nice day.







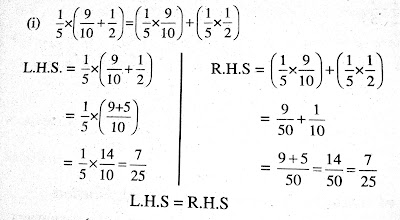


.jpg)
.jpg)

2 Comments
Wow!!!❤💚💛
ReplyDeleteNo words at all...Just amazing
Good effort Sir....keep it up....
ReplyDelete