Representing Sets through Venn diagrams

 

Representing Sets through Venn diagrams: وین ڈایگرامز

( venn diagrams were introduced by John venn a British philosopher )

A Venn diagram is a simple closed figure which shows the sets and their relationships.

In Venn diagrams we represent the universal set by a rectangle and the other sets are represented by a closed circle into the inner area of the rectangle. (which represent the universal set).

وین ڈایگرامز میں یونیورسل سیٹ کو مستطیل بکس میں ظاہر  کیا جاتا ھے۔اور باقی سیٹوں کو سادہ بند دائرہ کی شکل میں یونیورسل سیٹ کے اندر  ظاہر کیا جاتا ھے۔

Now we represent the different set operations in Venn diagrams.

Union of Sets:سیٹوں کا یونین 

If there are two sets, S and D. 

S ={1,2,3} , D ={ 1,2,3,4}

By observing elements of these both sets it is clear that set S is subset of set D and the union of these both sets is 

{ 1,2,3,4}

In Venn diagram we draw both the sets in a universal set and draw the set S in inner area of set D because S is subset of set D.

ہم دونوں سیٹوں کو یونیورسل سیٹ کے اندر اس طرح ظاہر کریں گے کہ سیٹ ایس کو سیٹ ڈی کے اندر بنائیں گے کیونکہ سیٹ ایس سیٹ ڈی کا تحتی سیٹ ہے۔

The Venn diagram of this example can be drawn as

Pic.

In Venn diagrams we shade the region on the basis of our result.

If set D is subset of set S then Venn diagram is represented by (in union)

اگر سیٹ ڈی سیٹ ایس کا تحتی سیٹ ہو تو وین ڈایاگرام کچھ اس طرح سے ہو گی۔

Pic.

If two sets are Overlapping sets: اگر دو سیٹ متراکب سیٹ ہوں 

In overlapping sets both sets have some common elements but not the elements of both sets are same. 

متراکب سیٹ ایسے سیٹ ہوتے ہیں جن کے چند ایک ارکان ایک جیسے ہوں پر سارے ارکان ایک جیسے نہ ہوں ۔متراکب سیٹ کہلاتے ہیں۔

Example, A={ 1,2,3,4,5 }  ,B ={ 2,4,6,8}

In union the result is { 1,2,3,4,5,6,8 }

So we shade the area of both sets

Pic.

If two sets are disjoint sets: اگر دو سیٹ غیر مشترک سیٹ ہوں۔

Disjoint sets have no common elements e.g A ={ 1,2,3,4}  ,C ={ 6,7,8 }

In union the result of these sets is

 { 1,2,3,4,6,7,8 }

So we shade the area of both sets.

غیر مشترک سیٹ ایسے سیٹ ہوتے ہیں جن کا کوئی بھی رکن ایک جیسا نہ ہو 

Pic.

Intersection of Sets: سیٹوں کا تقاطع 

سیٹوں کے تقاطع میں ہم سیٹوں کے مشترکہ ارکان جواب میں لکھتے ہیں۔

If A and B are two sets and A is subset of B ,it means all elements of A is present in set B.

By taking intersection the result is set A, so Venn diagram of these sets as

Pic.

If set B is subset of set A then by taking intersection of these sets the result is set B.

The Venn diagram is

Pic.

If set A and set B is overlapping sets متراکب سیٹthen taking the intersection of these sets the result is the common elements of A and B.

The Venn diagram is

Pic

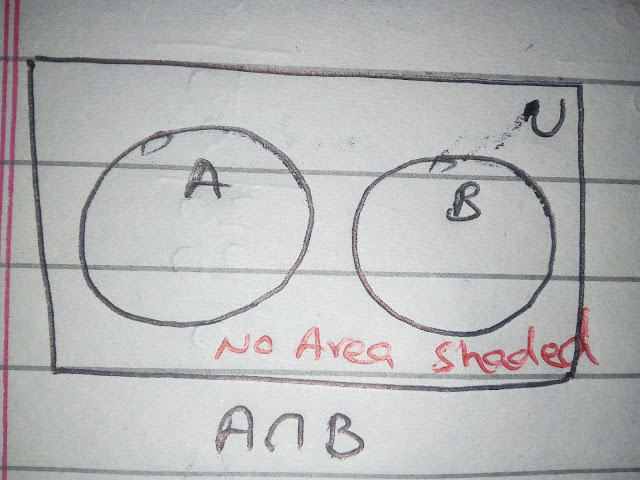
If set A and set B is disjoint sets غیر مشترک سیٹ then taking the intersection of these sets the result is a empty set so in Venn diagram we shade no area of these both sets. 

جب دو سیٹ غیر مشترک ہوں تو ان کا تقاطع لینے سے جواب خالی سیٹ آ تا ہے۔ اس کا مطلب ہم کوئی علاقہ شیڈ نہیں کریں گے۔

The Venn diagram is

Pic

Difference of two sets: دو سیٹوں کا فرق 

If set A and set B are two sets and set A is subset of set B, so when we take difference A - B ,the result is a empty set { }. In Venn diagram we shade no area.

The Venn diagram is

Pic

If set B is subset of set A and by finding A - B we get the elements of set A which are not present in set B so we shade the area of set A.

Venn diagram is

Pic

If set A and set B is overlapping sets متراکب سیٹ . If we find A - B the result is that elements of set A which are not present in set B.

If we find B - A then the result is that elements of set B which are not present in set A.

The Venn diagram in both conditions as

If set A and set B are disjoint sets غیر مشترک سیٹ then by taking A - B , the result is the elements of set A.

So we shade the area of set A. If we find B - A the the result is the elements of set B so we shade the area of set B.

The Venn diagram is

pic

Complement of a set: سیٹ کا کمپلینٹ 

If U is a universal set and other set A , the complement of set A is A' = U - A

In result we get the elements of universal set which are not present in set A so in Venn diagram we shade the area of set U and leave the area of set A.

Venn diagram,
Venn diagram of sets,
Venn diagram examples,
Venn diagram definition,
representative sets through Venn diagrams,
representing sets using Venn diagram,
what are the symbols in sets,
what does sets represent,
union of sets in Venn diagram,
union of sets Venn diagram calculator,
union of set using Venn diagram,
example of union sets in Venn diagram,
overlapping sets in Venn diagram,
overlapping sets examples,
overlapping sets,
overlapping sets symbols,
disjoint set in Venn diagram,
disjoint diagram of sets,
Venn diagram of subsets,
disjoint set meaning in Urdu,
intersection of set in Venn diagram,
examples of intersection of sets in Venn diagram,
what is intersection of sets examples,
difference of sets in Venn diagram,
Venn diagram of sets,
difference of sets in Venn diagram,
complement of set in Venn diagram,
what is the complement of set a,

Have a nice day.