INFORMATION HANDLING

Learning Outcomes:

After reading this post Readers will be able to:

1- Know about the Information Handling

2- How to collect Data and  represent Data?

3- Types of Data

4- Difference between grouped and ungrouped Data

5- Know about Horizontal and vertical bar graphs

6- About pie graph and how to draw pie graph

7- What is frequency and frequency distribution

8- How to draw histogram which represent frequency table

9- How to calculate Mean, weighted mean, median and mode

Information Handling

Introduction:

Information Handling is a branch of statistics which deals with the collection, analysis(تجزیہ), explanation (وضاحت) and presentation of data. The word statistics has been deduced from the Latin word Statisticum collegium that means council of state(ریاستی کابینہ) and the Italian word statista which means politician(سیاستدان).

In the world around us there are a lot of questions and situations (حالات) that we want to understand, describe, explore and access(رسائی ). 

For example

How many hospitals are there in out country?

How many children were born during the last ten (10) years?

How many doctors will be required in the next five years?

To know about such things, we collect information and present it in a manageable way( منظم انداز) so that useful conclusions (نتائج ) can be drawn. The branch of statistics that deals with this process is called information Handling (معلومات داری).

Data:

A data is a set of information and facts (حقائق ) which is represented in the form of figures. We can collect data by several ways, depending upon the quantity of the data and reason for it's collection. 

OR Data means facts or groups of information that are normally the results of measurements(پیمائش ), observations and experiments. These results help us in reviewing our past performance(کارکردگی ) and future planning. For example the government of a state prepares it's budgets (بجٹ) and development plans on the basis of a collected data about the resources and population.

Presentation of data:

After the collection of data the most important step is its presentation (ظاہر کرنا) that provides basis to draw conclusions. Data can be represented in the form of tables (جدول) and different kind of groups.

Ungrouped data:

The data that is collected in a raw form and it provides us information about individuals(انفرادی ). Data in such a form is called ungrouped data (غیر گروہی مواد).

Example:

11 players of a cricket team enhanced the score of the team in a one day match as given in following table.

Grouped data:

The data which provides us the information about groups is called the grouped data (گروہی مواد). For example we can represent the data of the above example in groups as,

Number of players who scored between 1-10=1

Number of players who scored between 11-20=2

Number of players who scored between 21-30=2

Number of players who scored between 31-40=5

Number of players who scored between 41-50=1

We can also represent (ظاہر کرنا) the above data by using a table as given below.

Graph:

A graph is a drawing that shows the relationship( تعلق) between numbers and quantities. We use graph to display a data in a simple, attractive and comprehensible (قابل فہم) way.

Types of graph:

There are two types of graph.

1- Bar graph

2- pie graph

Bar graph:

A graph in which data is represented by a number of rectangular bars (مستطیلی بار) is called a bar graph. A bar has a uniform width (چوڑائی ) and an equal distance from the other bars. we use two rays to draw a bar graph which are called axis and marking on axis is called it's scale. A graph with horizontal bars (افقی بار) is called horizontal bar graph and graph with vertical bars (عمودی بار) is called vertical bar graph.

Vertical bar graph:

We an understand this type of bar graph by an example.

John got the following marks out of 100 marks

Solution:

Choose a suitable scale (مناسب سکیل) to draw a graph.

Draw x-axis and  y-axis with the common point O.

Indicate marks according to the scale(سکیل), along y-axis

Along x-axis mark each month (ہر ماہ) after a suitable distance.

Draw coloured rectangular bars (رنگ دار مستطیلی بار) according to the scale for each month.

Pic

How to read bar graph:

1- The bar graph represent in general the marks of John that he got in six(6) tests.

2- January is the month in which John got the maximum marks.

3- September is the month in which John got the least marks.

4- The ratio of the marks of October to the marks of November is 80:60 or 4:3

5- The month of best performance is January and that of worst performance is September.

Horizontal bar graph:

Observe the following example

John traveled to help the poor as given in the following table.

Solution:

Choose a suitable scale (مناسب سکیل) to draw a graph.

Draw x-axis and y-axis with the common (مشترک) point O

Along y-axis mark each day after a suitable distance (مناسب فاصلہ)

Draw coloured rectangular bars according to the scale(سکیل کے مطابق) for each day.

How to read this bar graph:

1- The bar graph is representing in general the distance that John traveled in five(5) days.

2- Monday is the day in which John traveled the maximum distance.

3- Tuesday is the day in which John traveled the least distance.

4- the ratio (نسبت) of distance of Monday to the distance of Tuesday is 920:640 or 23:16

5- The day of maximum(زیادہ) traveling is Monday and that of least traveleing is Tuesday.

Pie graph: 

The representation of a numerical data in the form of disjoint sectors (قطعہ) of a circle is called a pie graph.

A pie graph is generally used for the comparison (موازنہ) of some numerical facts classified in different classes. In this graph the central angle measure 360 degree which is subdivided into the ratio (نسبت) of the size of the groups to shown through this graph.

Example:

Read the following pie graph which is showing the favourite fruit (پسندیدہ پھل) of 900 boys?( When pie graph is giving)

1- How many boys , favourite fruit is mango ?

2- How many boys , favourite fruit is banana?

3- How many boys , favourite fruit is apple ?

4- How many boys , favourite fruit is grapes ?

5- which fruit is the most favourite of the boys?

Solution:

We use the following formula (فارمولا) to solve it

Required quantity = (given angle/360)× total quantity

1- Mango is favourite fruit = (210/360)×900 boys = 525 boys

2- Banana is favourite fruit = (60/360) × 900 boys =150 boys

3- Apple is favourite fruit = (50/360) × 900 boys = 125 boys

4- Grapes as a favourite fruit = (40/360)×900 boys = 100 boys

EXAMPLE:

It is compulsory (ضروری) for each student to take part in different games. Out of 1800 students in school 750 play cricket, 200 students play badminton, 400 students play hockey and 450 students play football. In order to represent (ظاہر کرنا) their comparison(موازنہ), draw a pie graph. (When data is giving)

Solution:

Total students = 1800

Formula:

Required angle = (no. Of students play a game ÷ total students) ×360

Angle in pie graph for badminton = (200 / 1800)×360 = 40 degree

Angle in pie graph for cricket = (750/1800)×360 =150 degree

Angle in pie graph for hockey = (400/1800)×360 = 80 degree

Angle in pie graph for football = (450/1800)×360 = 90 degree

Construction of pie graph:

First of all Draw a circle of suitable radius.

Draw an angle of 40 degree for badminton ,150 degree for cricket, 80 degree for hockey and the remaining angle will be 90 degree which represent the football.

Frequency and frequency distribution

Frequency:(تعدد)

The number of times a value occur in a data is called frequency of that value.

Example:

15 students obtained marks out of 10 in a test as following

5,3,7,10,7,9,3,7,5,4,6,8,7,5,2

In this data the frequency of 3 marks is 2.

The frequency of 5 is 3.

The frequency of 7 marks is 4

Frequency distribution:(تعددی تقسیم کا جدول)

To write a data in the form of a table in such a way that the frequency (تعدد) of each class can be observed at once is called its frequency distribution(تعددی تقسیم کا جدول).

Construction of frequency distribution table:

We can understand this by an example,

There are 50 students and they got marks as following in a 60 marks test.

25,33,34,26,35,28,29,36,30,54,30,39,36,37,39,40,37,34,27,41,37,41,38,42,48,51,40,51,43,40,41,39,48,51,53,41,37,52,28,46,44,37,39,52,51,40,45,46,43,53

Make a frequency distribution table taking six(6) classes of equal size by tally marks.

Solution:

In data we find lowest value which is = 25

Highest value is data = 54

Total classes = 6

Size of class interval = ( highest value - lowest value) / (number of classes)

Size of class interval = (54-25)/6

Size of class interval = 29/6

Size of class interval = 5 ( approximately)

Example:

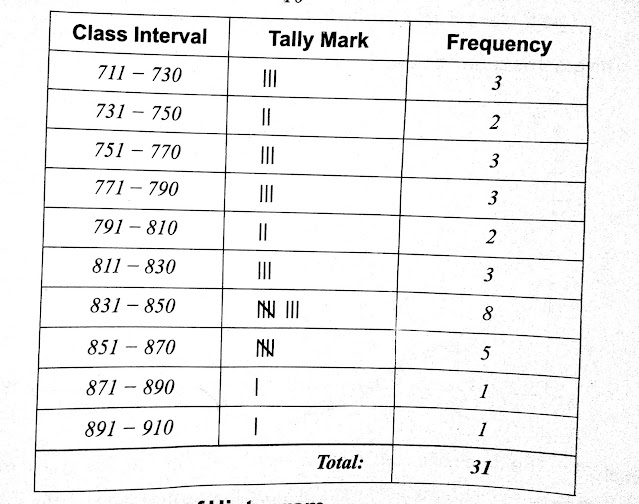
The number of units consumed electricity by 31 households are as following

727,773,859,711,860,747,862,738,774,852,791,836,834,752,828,792,908,839,752,715,880,838,

852,816,751,834,818,835,831,778,837. 

Make a frequency distribution table with 10 classes.

Solution:

Lowest value in data = 712

Highest value in data = 908

Number of classes = 10 

Class interval size = (908-711)/10

Class interval size = 197/10 = 19.7 = 20 (approximately)

Construction of Histogram:

We are familiar with pie and bar graph. Another common graphic way to presenting data is by means of histogram. A histogram is similar (same عکس) to bar graph but it is constructed for a frequency table.

In histogram the values of the data are represented along the horizontal axis and the frequency are shown by bars perpendicular to the vertical axis. Bars of equal width(چوڑائی ) are used to represent individual (انفرادی ) classes of frequency table.

To draw a histogram from grouped data the following steps are followed.

1- Draw x-axis and y-axis .

2- Mark class boundary of the classes along x-axis.

3- Mark frequency along y-axis.

4- Draw bar for each class so that the height of the bar drawn for each class is equal to the frequency of the class.

We can understand it by a example,

Example:

The detail of distances travelled (سفر کے تفصیل) daily by the residents of a locality are given below. Construct a histogram(کالمی نقشہ) for the following frequency table.

Solution:

The frequency distribution table is:

Histogram: (کالمی نقشہ)

Calculation of measures of central tendency:

Mean (average):

If x₁ ,x₂,.......,xₙ given quantities. Then their average or mean can be calculate by the following formula. ( X denotes Mean )

X = (x₁ + x₂ +......+xₙ) / n

X = (addition of all values)/ (number of values)

A student scores in eight papers are 58,72,65,85,94,78,87,85. Find the mean score.

X = ( 58+72+65+85+94+78+87+85) /8

X = 624/8 = 78

Hence the mean score is 78.

Weighted Mean: (اوزانی اوسط) 

When all values of given data have same importance then we use Mean(اوسط). But when different values have different importance then these values (اقدار) are known as weights.

If x₁,x₂,x₃,.......,xₙ have the weights w₁,w₂,w₃,.....,wₙ then

Weighted mean = Xw = (x₁w₁ + x₂w₂ + x₃w₃ + .........+ xₙwₙ ) / (w₁+w₂+.......+wₙ)

Example:

The following data describes the marks of a student in different subjects and their weights assign to these subjects are also given:

Find its weighted mean:

Solution:

Weighted mean = [ 4(74) + 3(78) + 5(74) + 6(90) ] / (4+3+5+6)

Weighted mean = ( 296+234+370+540)/(18)

Weighted Mean = 1440/18 =80 marks

Median : (وسطانیہ)

If some data is arranged in descending or ascending order then the median of the data is :

(a) The middle value of data , if it consists of odd number of values.

(b) If the data consists even values then the Median is the mean of two middle values.

Example:

Find the median if the weights in kg of 9 students are under as

29,32,45,27,30,47,35,37,33

Solution:

First we arrange these values in ascending order

27,29,30,32, 33, 35,37,45,47

The middle value is 33 So Median is 33 kg

Example:

Find the median if the weights in kg of 10 students are under as

29,32,45,27,30,47,35,37,33,31

Solution:

First we arrange these values in ascending order

27,29,30,31,32, 33, 35,37,45,47

so there are two values in the centre 

Median = (32+33)/2

Median = 32.2 ans

Mode: (عادہ)

Mode is the value that occurs (آنا) most frequently(سب سے زیادہ) in a data. In case no value is repeated (دہرانا) in data then the data (مواد) has no mode. When two or more values (اقدار) occur with the same greatest frequency , then each is a mode.

Example: Find the mode (عادہ) of the following data.

2,1,8,6,3,2,9,0,5,2,7,5,1,2

Solution:

Since 2 is repeated 4 times so this data has mode i.e 2

Example: find the mode of following data.

6,7,3,9,0,1,4,2

Solution:

This data has no mode because no value is repeated in this data.

Example: Find the mode of given data.

2,2,2,1,3,4,5,5,5,6,7

Solution:

In this data 2 is repeated 3 times and 5 is also repeated 3 times so this data has two modes i.e 5 and 2.

Note:

1- A data can have more than one mode(مواد کا ایک سے زیادہ عادہ ہو سکتا ہے).

2- A data may or may not have mode.

Have a nice day